量子傅里葉變換在 Shor 的整數分解算法中起什麼作用?
我似乎無法理解量子傅里葉變換在 Shor 的整數分解算法中的作用或目標。它是否用於將所有量子態坍縮成一個,其中它具有給定輸入的因子 $ n $ ?
為了進行分解,Shor 的算法提出了一種找到以下問題的方法。如果我知道一些自然數 $ g $ 和 $ N $ , 和 $ g < N $ , 在哪裡 $ \gcd(g, N) = 1 $ , 什麼是最小的 $ r > 0 $ 這樣 $ g^r = 1 \bmod N $ . 這被稱為尋找順序的問題 $ g $ 模組 $ N $ .
根據歐拉定理,會有一些這樣的 $ r $ 因為 $ g^{\phi(N)} = 1 \bmod N $ 對全部 $ \gcd(g, N) = 1 $ , 在哪裡 $ \phi(N) $ 是歐拉的總函式
量子計算的煩人之處,正如您可能已經發現的那樣,您可以創建一些任意的狀態疊加並並行計算所有這些狀態,但是當您想要獲得實際值時,您只能查看其中一個答案,從答案分佈中隨機選擇。比如說我們設置 $ a $ 是某種量子態,它是從 1 到 10 的所有整數的疊加(每個整數都具有相等的機率)。然後我們計算 $ b=2*a $ . 它將所有狀態並行乘以 2,我們將得到一個量子狀態,它是從 2 到 20 的所有偶數的疊加。現在,如果我們“打開”狀態 $ b $ 我們得到一個從 2 到 20 的隨機偶數。這沒什麼用。我們本可以打開 $ a $ 首先自己完成計算。
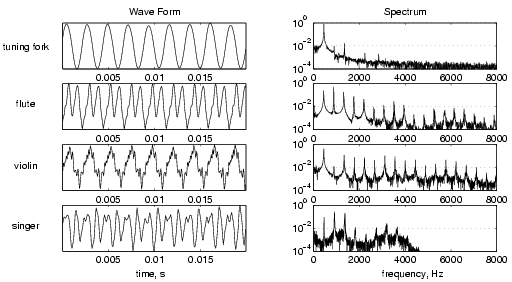
現在,傅里葉變換採用一個函式併計算它所組成的“波”。例如,下圖(來自本網站)顯示了不同儀器的波形及其相應的傅里葉變換。特別要注意傅里葉變換圖中的尖峰。第一個尖峰對應於函式的周期。其他尖峰顯示在此之上存在的各種諧波。
現在,回到尋找順序 $ g $ 模組 $ N $ . 你從設置開始 $ a $ 是從 0 到所有數的均勻疊加 $ q-1 $ , 對於一些 $ q >> N $ .
然後你計算 $ (a, g^a \bmod N) $ . 這將是一個疊加 $ q $ 元組。
現在是重要的部分。 $ g^a \bmod N $ 是周期性的。具體來說,如果 $ r $ 是最小的非零整數,使得 $ g^r = 1 \bmod N $ , 然後 $ g^a \bmod N $ 是周期性的 $ r $ . 所以,就像樂器一樣,如果你要繪製 $ a $ 反對 $ g^a \bmod N $ ,在此之上會有一些可見的重複基頻和許多其他諧波。所以現在如果你計算傅里葉變換 $ (a, g^a \bmod N) $ 您將獲得一個函式,顯示不同頻率出現的頻率。
現在我們看看保存頻率值的寄存器。我們有可能會得到一個高次諧波,但我們很有可能會得到基頻。這個頻率對應於週期 $ g^a \bmod N $ ,即 $ r $ . 由於這個實驗有一定的失敗機率(選擇一個高次諧波)。但是,如果你重複它一些多項式次數,你可以讓它在所有這些時間失敗的機率盡可能低。
TL;DR:非常簡單,量子傅里葉變換放大了周期性 $ p $ , 在哪裡 $ g^\frac{p}{2} - 1 = a $ 我們可以找到一個因子 $ N $ 通過執行歐幾里得算法 $ \text{Euclid}(a, N) $ .
Shor的算法一句話(基本上):
你從一些隨機猜測開始,這些猜測可能與 $ N $ (很可能不會)並且算法將第一個猜測“轉換”為更好的猜測,這確實與 $ N $ .
那麼你的猜測可能是一個直接因素 $ N $ (這也將是解決方案,因為 $ N = p \times q $ ),但不一定是,它也可以是一個與 $ N $ . 由於歐幾里得算法,這已經足夠了。使用歐幾里得算法,您可以通過非常基本的數學非常快速地找到兩個數字之間的公因數。
Shor 算法的技巧依賴於一個簡單的數學事實:
對於沒有公因數的兩個數 $ a $ 和 $ b $ , 存在一個數 $ m $ 和 $ p $ 以便$$ a^p - 1 = m \times b $$
( $ p $ 這裡只是一些數字,不是 $ p $ 從 $ N = p \times q $ ).
一個例子:
$ 7 $ 和 $ 15 $
$ 7^4 - 1 = 160 \times 15 $ .
因此對於 $ N $ 你會猜 $ g $ 並且可以保證一些數字 $ p $ 存在 $ g^p - 1 = m \times N $ .
還要注意 $ g^p - 1 $ $ \implies $ $ (g^\frac{p}{2} + 1) \times (g^\frac{p}{2} - 1) $ .
對於我們的例子 $ 7 $ 和 $ 15 $ :
$ 7^\frac{4}{2} - 1 = 48 $
然後我們使用歐幾里得算法來找到共享因子 $ 15 $ 和 $ 48 $ :
$ \text{Euclid}(15, 48) = 3 $ .
然後我們有了我們的解決方案,因為 $ 15 = 3 \times 5 $ .
但是量子傅里葉變換如何在其中發揮作用呢?
嗯,問題是你不能輕易找到號碼 $ p $ 使用經典電腦,您需要 $ p $ 使上述所有工作。
量子電腦可以通過使用稱為量子疊加的東西來計算一個輸入的許多可能答案。
但這也是一個問題,因為當你測量疊加時,你只能從量子電腦中檢索一個答案。它可能會給你一個錯誤的答案,因為所有答案都是均勻分佈的。
你可以取任何號碼 $ x $ 並得到一個餘數 $ r $ 通過執行計算:
$$ g^x = m \times N + r $$
**這裡重要的部分是這個剩餘部分 $ r $ 有周期性!**而這個週期性正是 $ p $ .
所以
$$ g^x = m_1 \times N + r $$
$$ g^{x+p} = m_2 \times N + r $$
$$ g^{x+2p} = m_3 \times N + r $$
$$ \vdots $$
注意如何 $ r $ 始終保持相同的數字。
所以我們現在看到,我們正在尋找的冪 p 具有重複屬性。
而這正是量子傅里葉變換發揮重要作用的地方,因為通過量子傅里葉變換,我們可以找到這種週期性 $ p $ .
我們仍然有所有可能的答案 $ p $ 在量子電腦的疊加中,但 QFT 消除了錯誤的答案(如降噪耳機消除了噪音)並放大了正確的答案。
一旦我們對量子電腦的量子態進行測量,我們就會得到單個量子態$$ \frac{1}{p} $$
然後我們可以反轉 $ \frac{1}{p} $ 並得到 $ p $ . 如果 $ p $ 即使我們最終可以找到一個數字(與 $ g^\frac{p}{2} - 1 $ ) 誰與 $ N $ . 我們使用歐幾里得算法得到公因數,那麼這個因數顯然是 $ N $ .
如果 $ p $ 甚至不是你必須用不同的數字再次猜測。平均而言 $ p $ 你在整個過程之後得到的機率是 $ 37.5 % $ 平的機會。