SHA-3 狀態數組索引背後的推理
我正在閱讀 SHA3 標準(https://dx.doi.org/10.6028/NIST.FIPS.202),在標準中它定義瞭如何從一維數組構造 3D 狀態數組。
狀態數組定義如下:
對於滿足 0 ≤ x < 5、0 ≤ y < 5 和 0 ≤ z < w 的所有三元組 (x, y, z),
一個
$$ x, y, z $$= S$$ w(5y + x) + z $$
這個索引有點麻煩,因為在某種意義上,y > x > z(如果需要,我可以澄清我的意思)。我認為交換 x 和 y 索引並將其定義為更自然:
一個
$$ x,y,z $$= S$$ w(5x + y) + z $$
標準中的定義是否有原因?
首先讓我們看一下狀態表示。
對於所有三元組 $ (x,y,z) $ 這樣 $ 0 \le x < 5 $ , $ 0 \le y < 5 $ , 和 $ 0 \le z < w $ ,
$$ A[x,y,z]=S[w(5y+x)+z]. $$ 例如,如果 $ b = 1600 $ , 以便 $ w = 64 $ , 然後
A[0,0,0] = S[0] A[1,0,0] = S[64] A[4,0,0] = S[256] A[0,0,1] = S[1] A[1,0,1] = S[65] A[4,0,1] = S[257] A[0,0,2] = S[2] A[1,0,2] = S[66] A[4,0,2] = S[258] A[0,0,61] = S[61] A[1,0,61] = S[125] A[4,0,61] = S[317] A[0,0,62] = S[62] A[1,0,62] = S[126] A[4,0,62] = S[318] A[0,0,63] = S[63] A[1,0,63] = S[127] A[4,0,63] = S[319] and A[0,1,0] = S[320] A[1,1,0] = S[384] A[4,1,0] = S[576] A[0,1,1] = S[321] A[1,1,1] = S[385] A[4,1,1] = S[577] A[0,1,2] = S[322] A[1,1,2] = S[386] A[4,1,2] = S[578] A[0,1,61] = S[381] A[1,1,61] = S[445] A[4,1,61] = S[637] A[0,1,62] = S[382] A[1,1,62] = S[446] A[4,1,62] = S[638] A[0,1,63] = S[383] A[1,1,63] = S[447] A[4,1,63] = S[639]如果您查看位的位置。您注意到您可以將您的狀態視為一個數組 $ \texttt{u_int64} $ (編號 $ 0 \to 63 $ , $ 64 \to 127, \ldots $ ),這解釋了 $ w $ 在公式。
如果您查看位的順序,您會注意到我們有第一個平面 ( $ y = 0 $ ),然後是第二個等等。因此取 320 個第一位選擇第一個平面,依此類推。
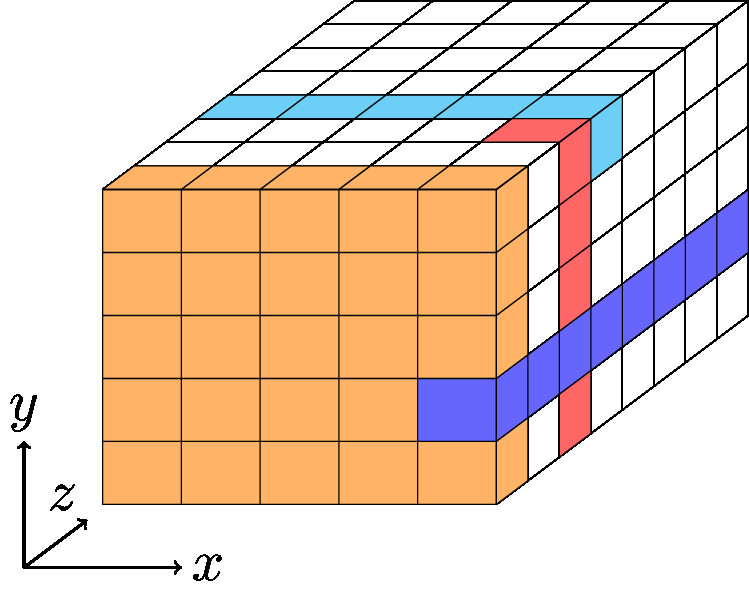
現在,如果您查看 Keccak 中的操作:
- $ \iota $ 在車道上操作 $ (0,0) $ ,
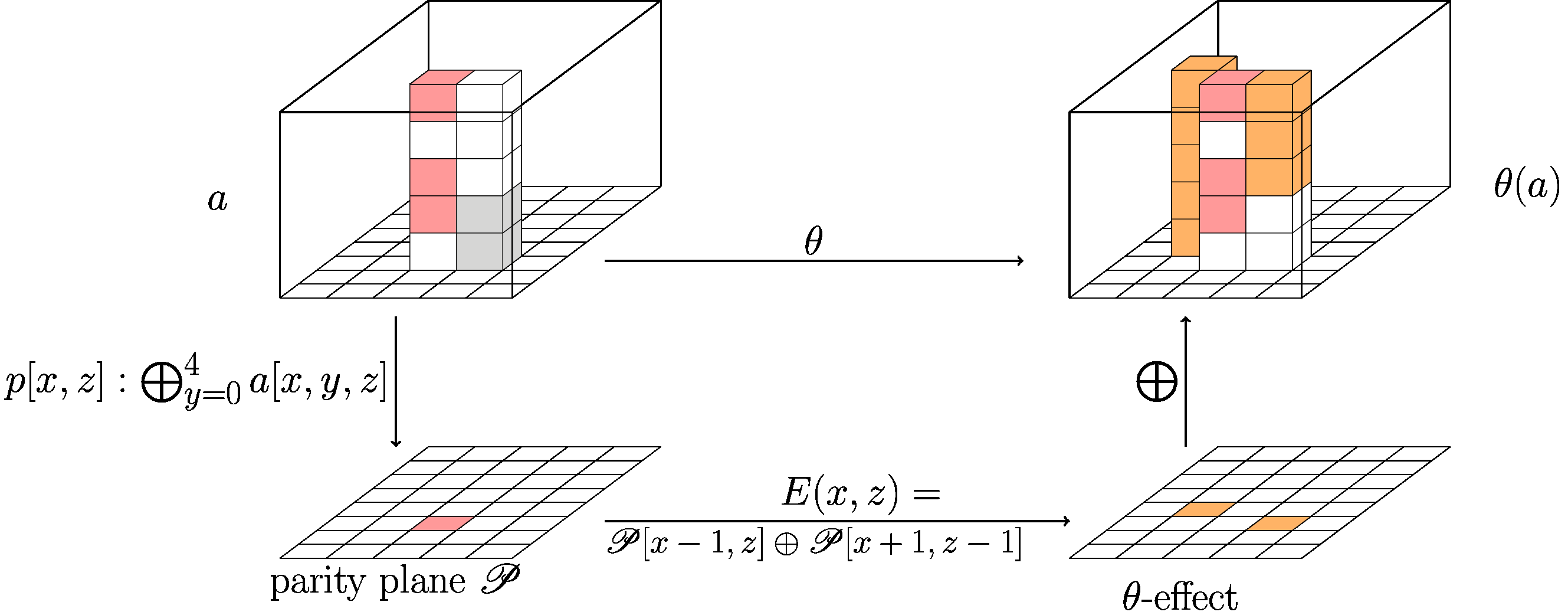
- $ \theta $ 對列進行操作,但取決於其相鄰列的奇偶性,
- $ \pi $ 和 $ \rho $ 直接在車道位置上操作
- $ \chi $ 應用於一行。
$ \chi $ 也可以看成是一個5位的S-box,經過位分片,待應用 $ 64 $ 並行時間(見下文)。
因此,我們可以選擇 320 位並應用 $ \chi $ 直接地,這些位以這樣的方式分組,即連續載入它們會很快(而不是在不同的位置獲取它們)。所以我們有第一個理由更喜歡這種排序。
然後我們可以看看 $ \theta $ ,它主要在列上工作,但您也可以考慮直接在平面上進行(因此並行 320 次!)。
因此,通過 320 位的塊選擇狀態並從向量的角度添加它們使其速度更快。
因此,我們在這裡有兩個操作( $ \theta $ 和 $ \chi $ ) 這極大地受益於 $ w(5y+x)+z $ 訂購。
現在,如果您假設其他順序( $ w(5x+y)+z $ ),請注意:
- 當你想申請時,你必須從 5 個不同的位置獲取位 $ \chi $ .
- 你只能工作 $ \theta $ 與列平行,不再是石板。
TL;博士: $ \chi $ 和 $ \theta $ 並行性從這種排序中受益匪淺(從硬體的角度來看也是如此)。